Sudoku is a logic-based, combinatorial number-placement puzzle. In classic sudoku, the objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid contain all of the digits from 1 to 9. The rules are simple: each number can only appear once in a row, column or subgrid. Sugolver is a Sudoku solver written in Go.
In this article is describing the data structures and the algorithms used in this project hosted on Github at this following URL: https://github.com/lunatikub/sugolver. Enjoy the read !
Terminology
In this sudoku solver post and github code we will use a specific terminology to describe the different aspects of the Sudoku solver. Firstly 9 lines, 9 columns and 81 cells composed the grid. Secondly a cell contains a digit from 1 to 9 at coordinates (x,y).
For instance, a grid is subdivided with 9 regions called blocks, each block is identified by an integer called BlockID. So a block is composed of 3 lines, 3 columns and 3×3 (9) cells.
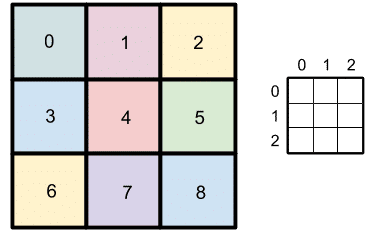
We can deduce a number of constants sufficient to describe the whole problem to be solved
const ( nrLine = 9 nrCol = 9 nrBlock = 9 nrVal = 9 nrBlockLine = 3 nrBlockCol = 3 )
And the two main data structures used in this project are: solver and cell.
type cell struct { }
type Solver struct { }
Candidates
One of the first things to do is to determinate the potential candidates for each cell. The algorithm is:
for each empty cell of the grid {
for each value from 0 to 9 {
if the value is not on the cell's line, column and block {
add it to the set of the cell candidates
}
}
}
The number of candidates can be considered as the scale of complexity for the Sudoku to resolve from 0 (solved grid) to 9x9x9 = 729 (no initial value).
// File: solver.go func (s *Solver) setCandidates()
Another useful method is when we set a value V to a cell, we have to update the candidates of all cells of the same line, column and block, by removing the value V of the respective set of candidates.
// File: solver.go func (s *Solver) updateCandidates(line int, col int, v int)
Deductive rules
The rules of the game allow us to deduce other deductive rules named which will be applied for the resolution of the problem and which can be sufficient to resolve the whole problem when the complexity of the grid is not too high.
Exclusivity
If we have found the value V of a cell C then this value is removed from all cases in the same block as C, in other words we update the lines, the cols and the block Boolean vectors.
// File: exclusivity.go func (s *Solver) Exclusivity()
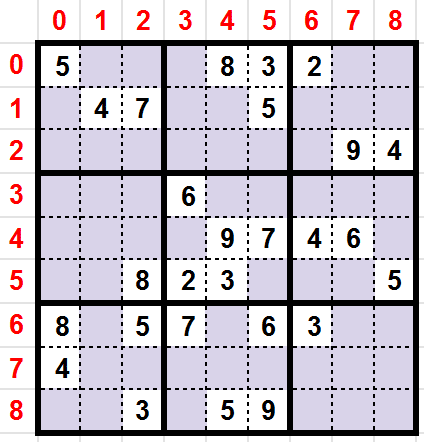
In the previous example (Candidates), we can see that the candidate at coordinate (y:2, x:3) can be set as the value 1. Consequently we have to update all candidates for the cells on the line:2, the column:3 and the block:1 by removing the value 1 from the respective set.
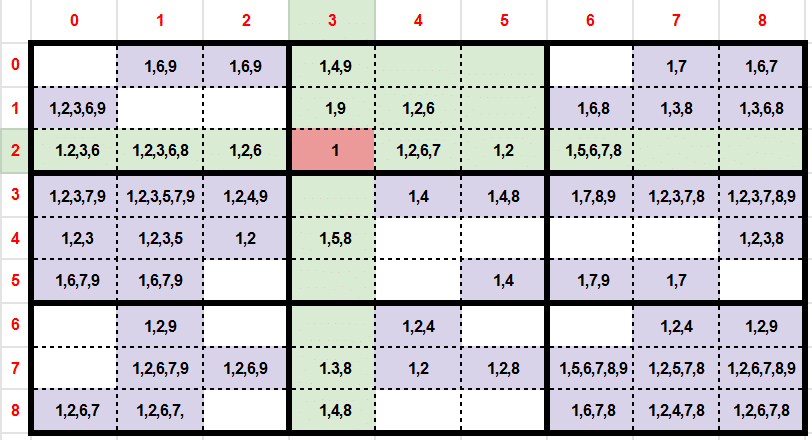
On the previous grid we have 195 candidates. After having updated the candidates, we have removed 13 candidates, so we lower the complexity of the grid and have found a new value.
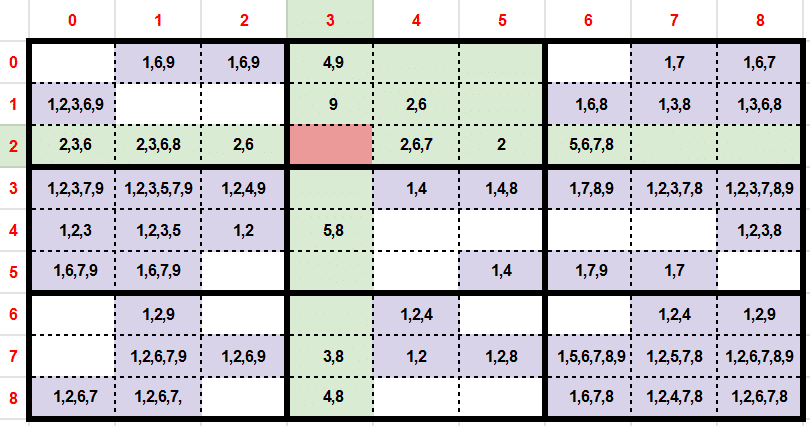
After the candidates updates, we notice that the cells (y:1,x:3) and (y:2,x:5) became exclusivity cells also. Then we do the same process by updating candidates. So the value 2 (y:2, x:5) removes 7 candidates. So the value 9 (y:1,x:3) removes 3 candidates.
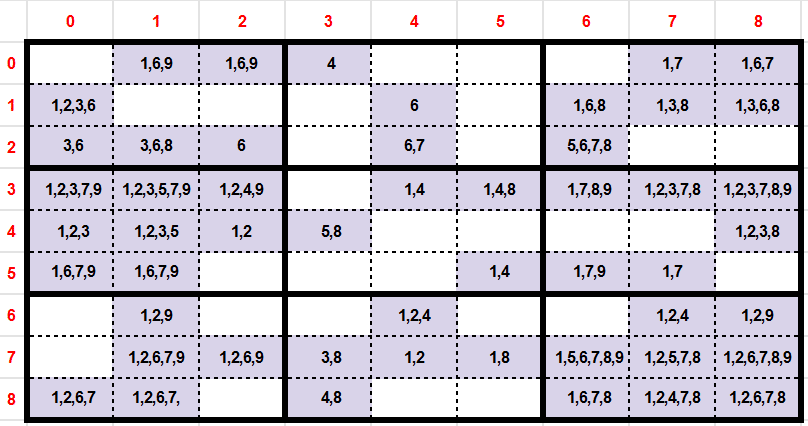
We notice that we have more exclusivity cells at each iteration
[ (y:2,x:2), (y:0,x:3), (y:1,x:4) ]. Certainly this Grid can be resolved entirely by this rule.
Take a look on at resulting grid after we have set the three new values deduced from the Exclusivity rule.
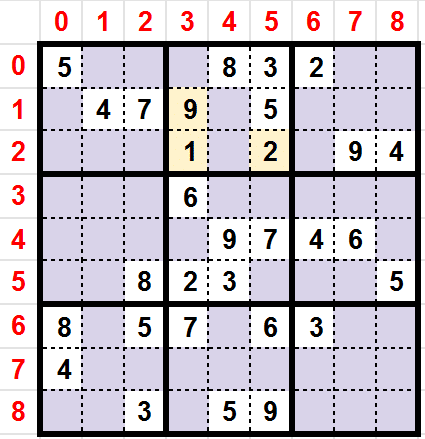
Uniqueness
If a cell C can contain several values, but one of these values V is not possible in any other cell of its line or columns or block, then cell C contains the value V
// File: uniqueness.go func (s *Solver) Uniqueness()
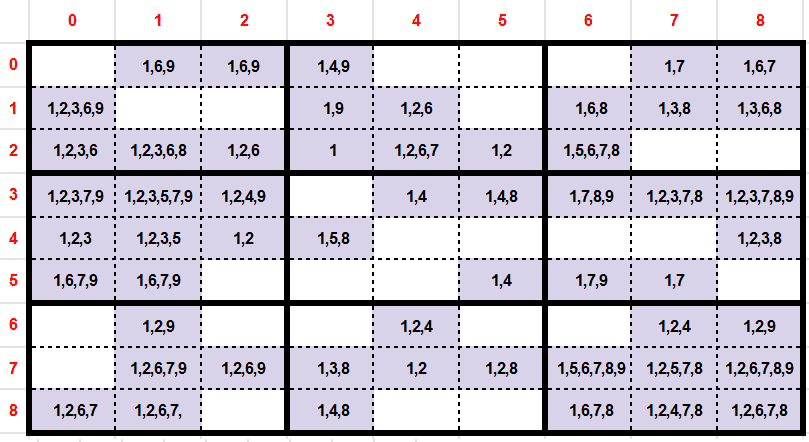
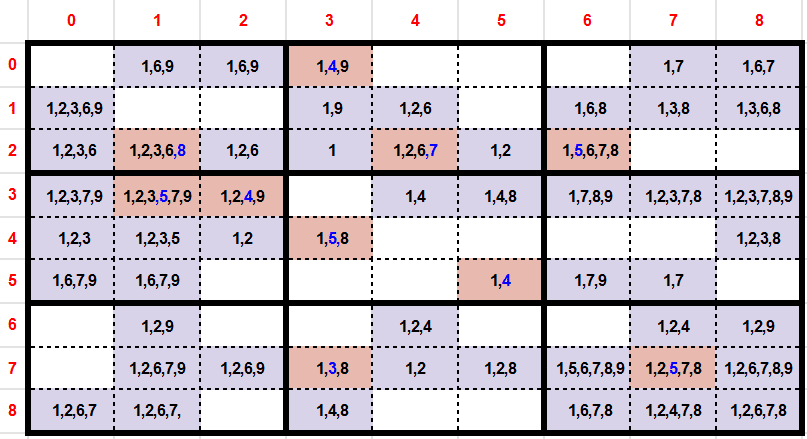
In the previous example (Candidates), we can see that the following candidates are respecting this rule:
- 4 in cell (y:0,x:3)
- 8 in cell (y:2,x:1)
- 7 in cell (y:2,x:4)
- 5 in cell (y:2,x:6)
- 5 in cell (y:3,x:1)
- 4 in cell (y:3,x:2)
- 5 in cell (y:4,x:3)
- 4 in cell (y:5,x:5)
- 3 in cell (y:7,x:3)
- 5 in cell (y:7,x:7)
Parity
If a couple of cells (C,C’) on the same line or on the same column or in the same block can only contain the same pair of values {U,V} then we remove these two values of the candidates from lines, cols and blocks of C and C’ cells candidates.
// File: parity.go func (b *Board) Parity()
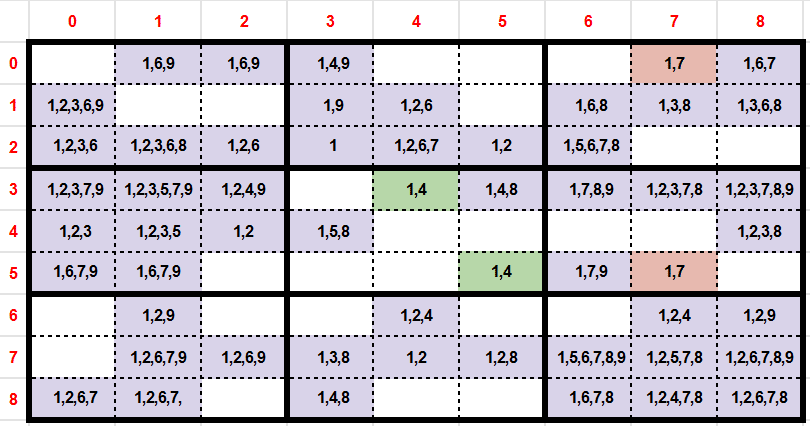
In the previous example (Candidates), we can see that the following cells are respecting this rule:
- Couple (C,C’): (y:0,x:7), (y:5,x:7) with {U,V} = {1,7}
- Couple (C,C’): (y:3,x:4), (y:5,x:5) with {U,V} = {1,4}
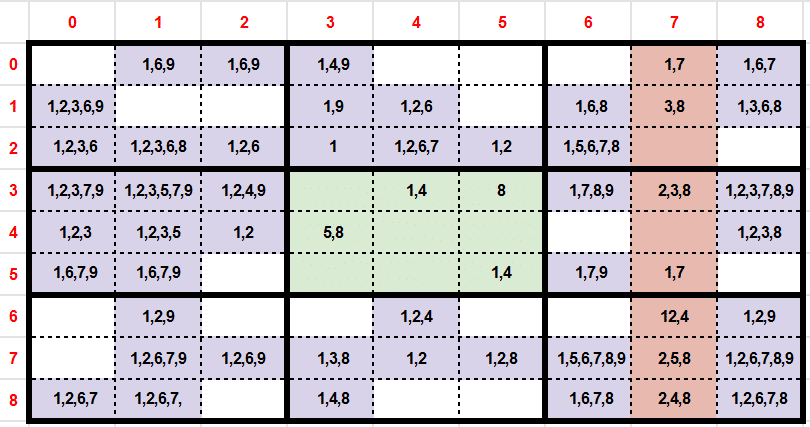
We respectively remove both values {U,V} from all the cells of the block and the column. As you can see, the block 4 has a new exclusivity cell (y:3, x:5), that will create an other exclusivity cell (y:4,x:3) and so on. So the two couples we removed 11 candidates.
Locked
This rule is not implemented yet
If in a block all candidates of a certain value are confined to a row or column, then the value cannot appear outside of that block in that row or column.
In the following example of candidates, we can see that the candidate 5 of the cell (y:2,x:6) can be removed.
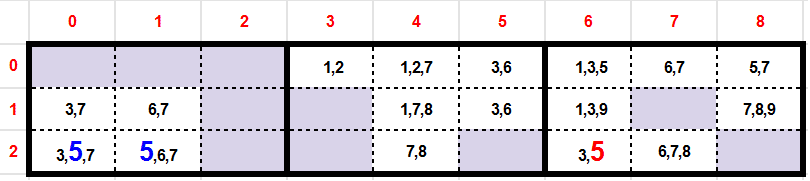
This previous rule is named locked pointing. Moreover an other variant exists, and it is named lock claiming. This one works exactly the other way round:
If in a row or a column all candidates of a certain value are confined to one block, then the candidate can be eliminated from all other cells in that block.
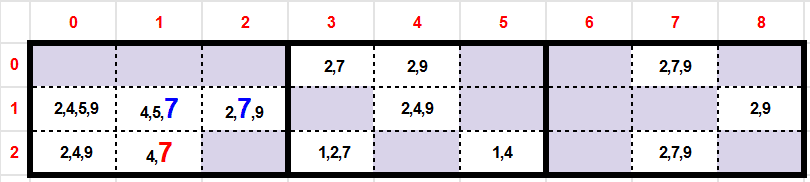
Backtracking
Sometimes, when the complexity of the grid is to higher, we have to finish the solving of the Sudoku by trying all possibilities with the candidates. Therefore we use backtracking as the algorithm.
// File: backtracking.go func (s *Solver) backtracking() bool
Note that the backtracking itself is enough to resolve any grid, if at least one solution exists, but it is less performant.
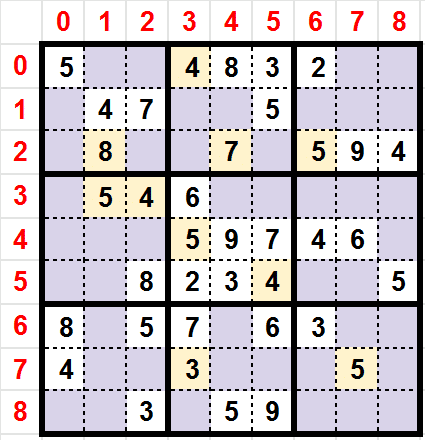
Take one of the simplest example of grid in order to explain how we process the backtracking.
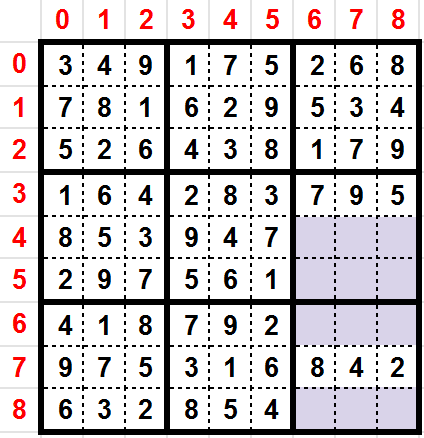
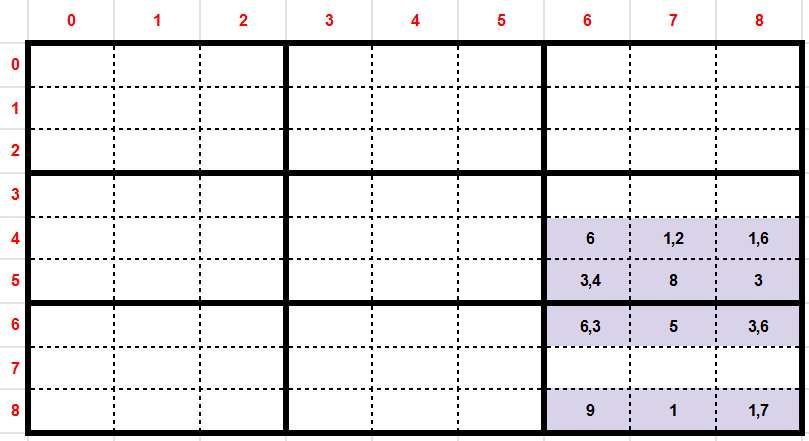
Following algorithm is applied (backtracking) on the previous example grid. For instance, we have isolated the sub block 5 and 8 to simplified the demonstration.
backtracking() {
for each empty cell C {
for each candidates V {
if set V is valid {
set V
backtracking()
reset C
}
return // no set available for this cell so backtrack !
}
}
// A solution has been found here !
}
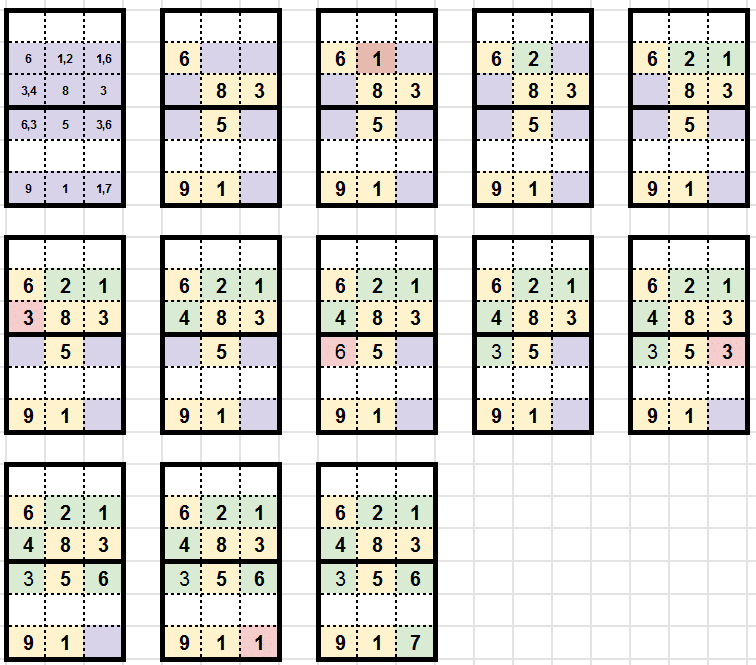
Step by step backtracking algorithm, we find a solution !
Solve
Now we have all the keys to have a sudoku solver !
Solve(initialValues [9][9]int) {
var G grid = init(initialValues)
do {
nrExclu = exclusivity(G)
nrUniq = uniqueness(G)
nrParity = parity(G)
} while (nrExlcu != 0 or nrUniq != 0 or nrParity != 0)
if G is not completed {
backtracking(G)
}
}
For practical reasons (benchmark purpose), we can disable each of the three EUP rules when we solve a Sudoku.
// File: solver.go func (s *Solver) Solve(doExclu bool, doUniq bool, doParity bool)
BenchMark
I have made a benchmark of the sudoku solver in order to compare performance on the resolution of a grid with and without the EUP rules applied.
Hardware which has been used:
- Latitude E7450 (062E)
- Intel(R) Core(TM) i7-5600U CPU @ 2.60GHz
- 2x8GiB SODIMM DDR3 Synchronous 1600 MHz
Kernel/distribution which has been used:
❯ uname -a Linux dune 4.15.0-115-generic #116-Ubuntu SMP Wed Aug 26 14:04:49 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux ❯ cat /etc/lsb-release DISTRIB_ID=Ubuntu DISTRIB_RELEASE=18.04 DISTRIB_CODENAME=bionic DISTRIB_DESCRIPTION="Ubuntu 18.04.4 LTS"
Command which has been used:
perf stat -e cycles
The following table summarizes the results. So each line is an average of 1000 iterations on 10 different grids.
| difficulty | rules enabled | cycles | time (us) |
|---|---|---|---|
| simple | no | 41899368 | 13493437 |
| simple | yes | 2423307 | 924195 |
| easy | no | 27989367 | 9115144 |
| easy | yes | 3303663 | 1235379 |
| intermediate | no | 97155979 | 30944644 |
| intermediate | yes | 3389270 | 1275257 |
| expert | no | 96257177 | 30630902 |
| expert | yes | 5236318 | 1855740 |
We notice two important things:
- The performance resolution is always better with the EUP rules applied
- The more complex the grid is the higher the gain will be.
Feel free to leave a message for any questions or suggestions, I’ll be more than happy to answer or can contact me at: contact@algomaths.tech
[bws_google_captcha]

