I spent a lot of my time a few years ago playing this game. Certainly one of the most addictive game! Moreover, the learning phase is very short and you quickly enjoy playing. But after many games you realize that it becomes difficult to go further. Therefore, you have to change the strategy you used to achieve it. Above all I tried to resume many reflections in my bot 2048.
The goal of this project is not to have the perfect bot 2048 but a comprehensible code, strategy and algorithms. Moreover I tried to detail and explain all aspects. It is often more difficult to keep the solution simple.
We will touch on the following aspects in this bot 2048 article:
- Bitwise operators in Golang.
- Expectiminmax algorithm.
- Heuristic evaluation of a 2048 board.
- Optimization by precomputed some values in Python.
This project is written in Go and hosted on Github at this following URL: https://github.com/lunatikub/bot2048.
Enjoy the read !
Game play 2048
2048 is played on a 4×4 grid, with numbered tiles that slide when a player moves them using the four arrow keys. At every turn, a new tile will randomly appear in an empty spot on the board with a value of either 2 or 4. Tiles slide as far as possible in the chosen direction until they are stopped by either another tile or the edge of the grid. If two tiles of the same number collide while moving, they will merge into a tile with the total value of the two tiles that collided. The resulting tile cannot merge with another tile again in the same move. You can play the game here.
Board encoding

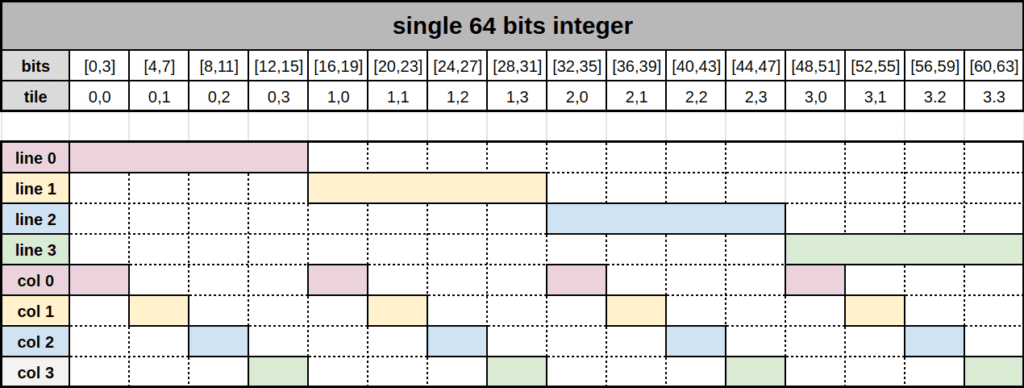
A board has 4 lines, 4 columns and 16 (4×4) tiles from the top left corner at coordinate {y:0,x:0} to the bottom right corner at {y:3, x:3}. So the implementation approach is to encode an entire board as a single 64 bits integer, where the tiles are the nibbles (i.e. 4-bit chunks) and a single line or a column is a 16-bit quantity. Further a nibble, with 4 bits, can take 16 different values from 0x0 to 0xf (0000 to 1111 in base-2 numeral system). So we cannot store directly the value of a tile but we can store his power of 2. With this strategy a tile can take a value from ![]() . However in the real world
. However in the real world ![]() but in our case
but in our case ![]() , I know it’s a mathematical aberration but it simplifies the implementation.
, I know it’s a mathematical aberration but it simplifies the implementation.
The aim is to optimize as maximum the memory and CPU to allows the AI to search through a huge number of game states in the shortest period of time because:
- Avoid a full structure implementation with all methods to copy/duplicate/compare…
- A board can be easily duplicated by a simple assignment “=”.
- Two boards can be easily compared by the operator “==”.
- On a 64-bit machine, this enables the entire board to be passed around in a single machine register.
- A table of size 65536 can encode all the transformations which operate on a single line/column (see move chapter).
Tile
Bit shift operations are used to extract individual tiles. Firstly we have to process the shift value in order to extract a tile: ![]() . Let’s take some examples:
. Let’s take some examples:
We precomputed all the shifted values in a slice to have a direct access from coordinates:
var shiftTile = [][]int{
{60, 56, 52, 48},
{44, 40, 36, 32},
{28, 24, 20, 16},
{12, 8, 4, 0},
}
Now we can easily get or set a tile with the appropriate mask applied.
func Set(b uint64, y, x, v uint8) uint64 {
n := shiftTile[y][x]
b &= ^(nibbleMask << n) // clear the nibble
return b | uint64(v)<<n // set the nibble
}
func Get(b uint64, y, x uint8) uint8 {
return uint8(b >> shiftTile[y][x] & nibbleMask)
}
Line
Bit shift operations are used to extract individual lines. As the tile, we precomputed the shifted values in a slice with the following formula: ![]() .
.
var shiftLine = []int{48, 32, 16, 0}
Now we can easily get/set a line, here we don’t need to apply a mask with the explicit cast.
func setLine(b uint64, y uint8, l uint16) uint64 {
n := shiftLine[y]
b &= ^(lineMask << n) // clear the line
return b | uint64(l)<<n // set the uint16
}
func getLine(b uint64, y uint8) uint16 {
return uint16(b >> shiftLine[y])
}
Column
It is a little bit complicated for the column because the values are not neighbors (single 64 bits integer schema). So for the “get” method, we build an 16-bit integer by getting tile one by one. And for the “set” method, we extract one by one the tiles from the 16-bit integer representing a column.
func setCol(b uint64, x uint8, c uint16) uint64 {
b = Set(b, 0, x, uint8(c>>(lineBits-nibbleBits)&nibbleMask))
b = Set(b, 1, x, uint8(c>>(lineBits-2*nibbleBits)&nibbleMask))
b = Set(b, 2, x, uint8(c>>(lineBits-3*nibbleBits)&nibbleMask))
b = Set(b, 3, x, uint8(c&nibbleMask))
return b
}
func getCol(b uint64, x uint8) uint16 {
return uint16(Get(b, 0, x))<<(lineBits-nibbleBits) |
uint16(Get(b, 1, x))<<(lineBits-2*nibbleBits) |
uint16(Get(b, 2, x))<<(lineBits-3*nibbleBits) |
uint16(Get(b, 3, x))
}
Move
There are four available moves in 2048 game:
- Right

- Left

- Up

- Down

Here an example of a right move on an initial line: {1, 0, 0, 1}. Don’t forget that the real value is the power of 2 of the nibble value.
We can admit a move is a transformation from a 16-bit integer to a 16-bit integer. In this example, from {1,0,0,1} (0x1001) to {0, 0, 0, 2} (0x2). For instance a simple deduction can be done, a table of size ![]() (UINT16_MAX) can encode all the transformations which operate on a single line or a column. To optimize the implementation we precompute all the transformations with a script transformation.py. This last generates 2 slices, one for the Right/Down transformations, one for the Left/Up transformations where the index is the line/column input and where the value is the output line/col of the transformation.
(UINT16_MAX) can encode all the transformations which operate on a single line or a column. To optimize the implementation we precompute all the transformations with a script transformation.py. This last generates 2 slices, one for the Right/Down transformations, one for the Left/Up transformations where the index is the line/column input and where the value is the output line/col of the transformation.
This script has a base function to transform 2 tiles:
def trans(n, m):
"""
transformation between 2 tiles
[n,m] -> [n',m']
"""
# merge
if n == m and n != 0 and n < 15:
return 0, n + 1, True
# move
if m == 0:tables
return 0, n, False
# nothing to do
return n, m, False
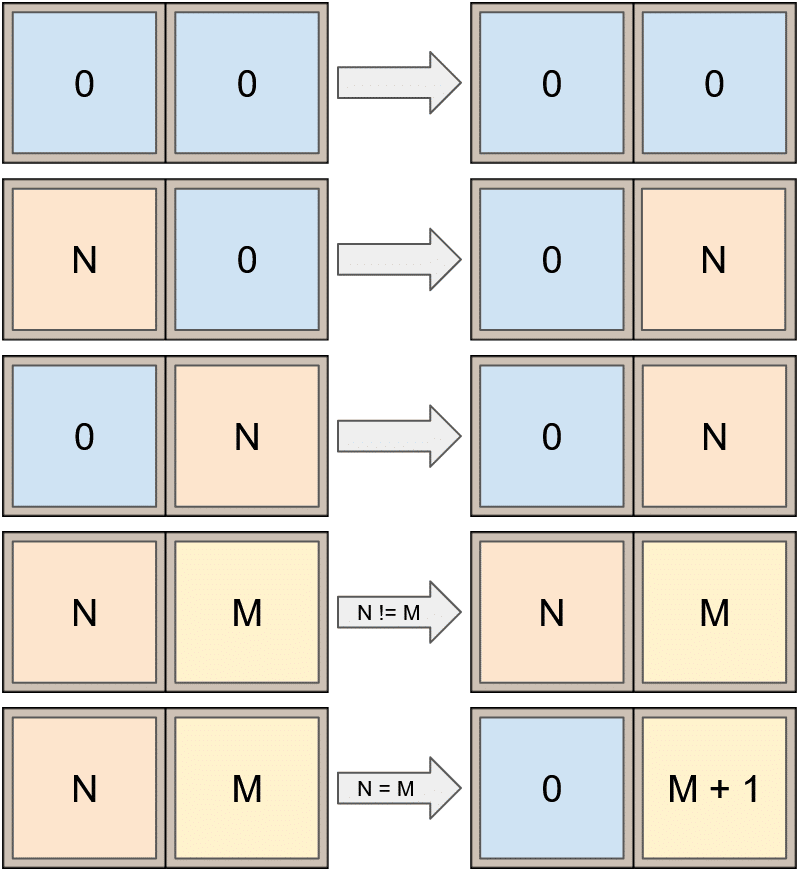
Therefore we have to apply this transformation for each tiles couple of a line or a column with a specific order. Let’s take the example for the right/down transformations (left/up are being symmetrical).
def transRightDown(a, b, c, d):
c, d, m1 = trans(c, d)
b, c, m2 = trans(b, c)
if not m1 and not m2:
c, d, m1 = trans(c, d)
a, b, m3 = trans(a, b)
if not m2 and not m3:
b, c, _ = trans(b, c)
if not m1 and not m2:
c, d, _ = trans(c, d)
return a, b, c, d
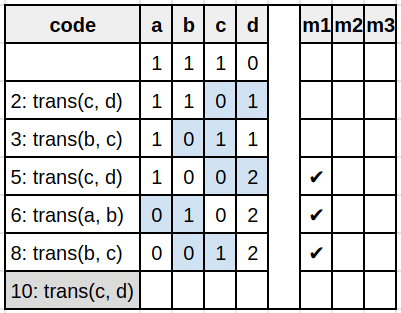
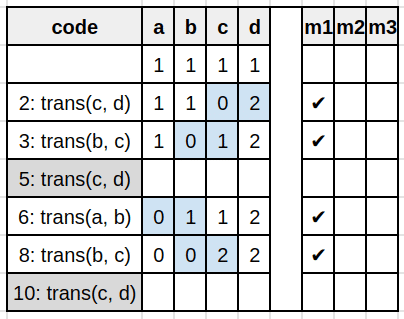
Therefore we can generate the transformation.go file:
// auto-generated file by `transformation.py`.
// Do not update it !
b, c, _ = trans(b, c)
var transLeftUp = []uint16{
0, 4096, 8192, 12288, 16384, 20480, 24576, 28672,...
4608, 4864, 5120, 5376, 5632, 5888, 6144, 6400, 6656, ...,
...
}
var transRightDown = []uint16{
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1, 2, 18, 19, 20, 21,...
39, 40, 41, 42, 43, 44, 45, 46, 47, 3, 49, 50, 4, 52, 53, 54, 55, 56, 57,...
...
}
Therefore it is really simple to apply a move to a column or a line only with an affectation. Let’s take an example with the left move. Then we apply the transformation on each line from 0 to 3 and set it in place.
func moveLeft(b uint64) uint64 {
b = setLine(b, 0, transLeftUp[getLine(b, 0)])
b = setLine(b, 1, transLeftUp[getLine(b, 1)])
b = setLine(b, 2, transLeftUp[getLine(b, 2)])
b = setLine(b, 3, transLeftUp[getLine(b, 3)])
return b
}
Bot 2048 AI
In the literature, almost all the works aimed at designing artificial players (like my bot 2048) are based on an evaluation function and a tree of possibilities. Firstly we will explain the heuristic to board scoring. Secondly we will see the Expectiminimax algorithm which is creating the tree of possibilities. Unlike a sudoku solver where there is no place for random, the bot 2048 with AI can make mistake because the decision cannot be the best, due to many things, like the random placement of the tile after each move or the limited depth of the algorithm.
Heuristic board scoring
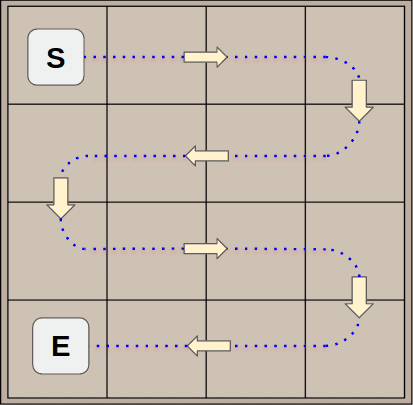
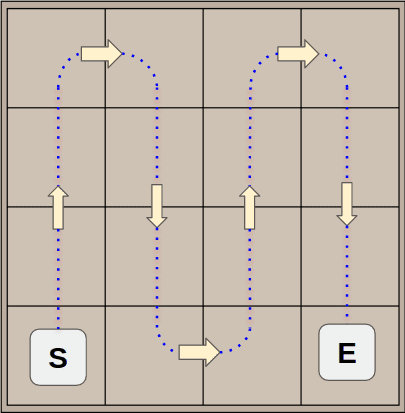
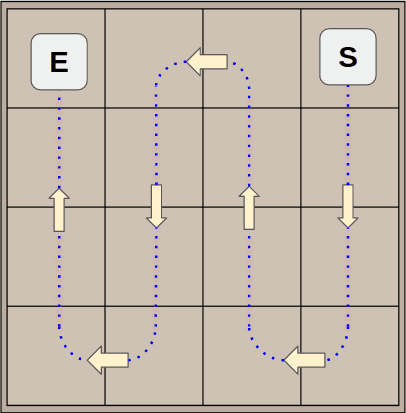
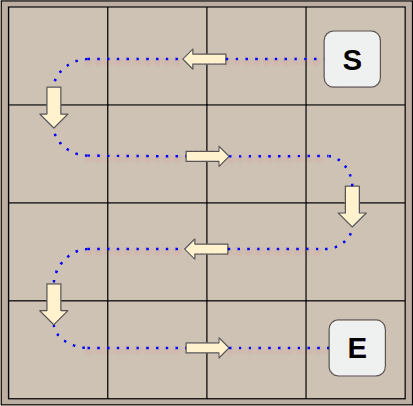
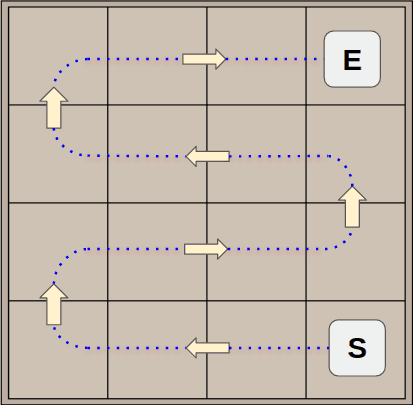
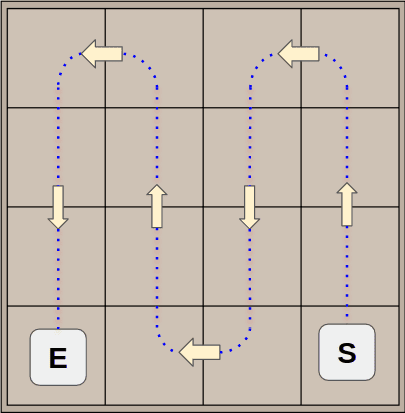
The assumption on which the scoring algorithm is based is rather simple: if you want to achieve higher score, the board must be kept as tidy as possible. In particular, the optimal setup is given by a linear and monotonic decreasing order of the tile values. There are 8, and only 8 different paths to browse all the tiles of a board (S: start, E: end).
In order to optimize the evaluation of a board, a python script path.py pre-computes and generates these paths with a simple algorithm. In input it takes an origin coordinate {y,x}, a main and a secondary direction among the following values: Right/left/Up/Down. Firstly we have to lookup for the next tile by applying the main direction.
For example:
- The tile is at {y:2,x:2} , and the main direction is Right and the secondary is Up.
- We apply the main direction, so the next tile will be at {y:2,x:3}.
- We apply again the main direction, the next tile will be at {y:2, x:4}, but {x:4} is out of bounds, so we apply the secondary direction.
- The result tile is at {y:1; x:3}.
- To end, we update the main direction by inverting from Right to Left.
Here we are with the following inputs of different paths for the script:
data=[
[(0, 0), Direction.RIGHT, Direction.DOWN],
[(3, 0), Direction.RIGHT, Direction.UP],
[(0, 3), Direction.LEFT, Direction.DOWN],
[(3, 3), Direction.LEFT, Direction.UP],
[(0, 0), Direction.DOWN, Direction.RIGHT],
[(0, 3), Direction.DOWN, Direction.LEFT],
[(0, 3), Direction.UP, Direction.RIGHT],
[(3, 3), Direction.UP, Direction.LEFT],
]
Then the output Golang file generated:
// auto-generated file by `path.py`.
// Do not update it !
var paths = [][]Tile{
{{0, 0}, {0, 1}, {0, 2}, {0, 3}, {1, 3}, {1, 2}, ... },
{{3, 0}, {3, 1}, {3, 2}, {3, 3}, {2, 3}, {2, 2}, ... },
{{0, 3}, {0, 2}, {0, 1}, {0, 0}, {1, 0}, {1, 1}, ... },
.....
}
To enforce the ordination of the tiles in a monotonic decreasing order, the score is computed as the sum of the linearized values on the board multiplied by the values of a geometric sequence with a weight.
![]()
![]()
![]()
All the height paths could be evaluated at once, the final score is the maximum score of any path.
const (
ratio = 2
weight = 100000
)
func eval(board uint64) int {
maxScore := -1
for _, path := range paths {
w := weight
score := 0
for _, tile := range path {
v := Get(board, tile.y, tile.x)
score += pow2[v] * w
w /= ratio
}
if score > maxScore {
maxScore = score
}
}
return maxScore
}

[(0, 0), Direction.RIGHT, Direction.DOWN],
Expectiminmax
Therefore we are able to evaluate a board, we have to create the tree of possibilities. Consequently we will use the expectiminimax (more precisely a expectimax). This algorithm is a variation of the minmax. The levels of the tree alternate between max nodes (player moves) and chance nodes (random sets) until the depth limit of the tree has been reached. Each “turn” of the game is evaluated as a “max” (representing the AI player’s turn) and a “chance” node as a “min” (representing the board’s turn).
const (
Board = iota
Player
)
func expectIMax(board uint64, depth, agent int) (int, int) {
if depth == 0 {
return eval(board), 0
}
if agent == Player {
return expectIMaxPlayer(board, depth)
}
return expectIMaxBoard(board, depth)
}
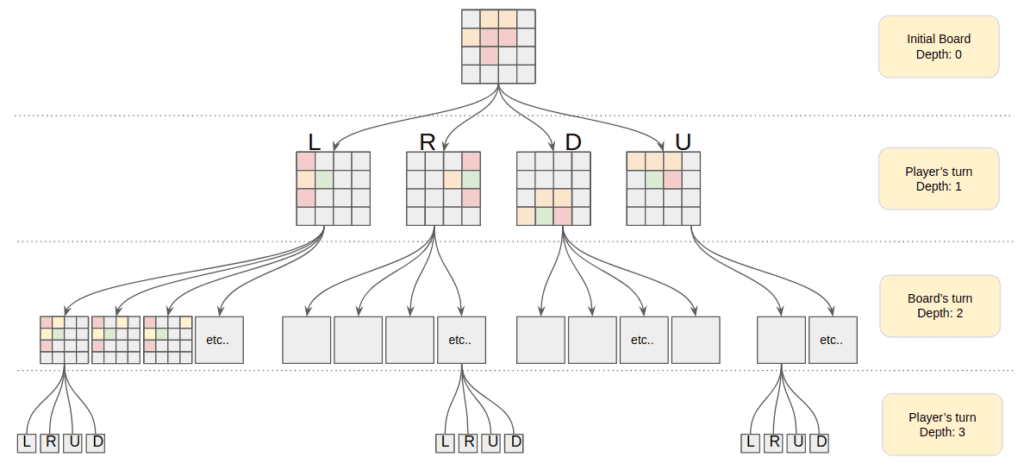
Player turn
The player’s turn can be resumed by creating 4 new nodes (4 boards) related to the 4 moves.
func expectIMaxPlayer(board uint64, depth int) (int, int) {
score := -1
move := 0
for m := range moves {
newBoard := Move(board, m)
if newBoard == board {
continue
}
newScore, _ := expectIMax(newBoard, depth-1, Board)
if newScore > score {
score = newScore
move = m
}
}
return score, move
}
Board’s turn
The board’s turn can be resumed by creating 2 new nodes (board) for each empty tile, one filled by a 2 and the second by a 4.
func expectIMaxBoard(board uint64, depth int) (int, int) {
score := -1
tiles := GetEmptyTiles(board)
for _, tile := range tiles {
newBoard := Set(board, tile.y, tile.x, 2)
newScore, _ := expectIMax(newBoard, depth-1, Player)
if newScore != -1 {
score += (newScore * 10) / 100 // 10% to pop 4
}
newBoard = Set(board, tile.y, tile.x, 1)
newScore, _ = expectIMax(newBoard, depth-1, Player)
if newScore != -1 {
score += (newScore * 90) / 100 // 90% to pop 2
}
}
score /= len(tiles)
return score, 0
}
Best move
By recursion the best move will be chosen when all possibilities will be evaluated
We only evaluate the board for each final node (when the maximum depth is reached).
func GetBestMove(board uint64, depth int) int {
_, move := expectIMax(board, depth, Player)
return move
}
The bot 2048 is now able to play:
- evaluate the board
- do the best move
- randomly set a tile (90% chance with a 2 and 10% chance with a 4).
- until a move is available: do it again
for {
move = bot.GetBestMove(board, opts.depth)
board = bot.Move(board, move)
empty := bot.GetEmptyTiles(board)
if len(empty) == 0 { // game over
break
}
board = bot.SetRandomTile(board, empty)
}
Conclusion
My bot 2048 is doing the job as I wished! Of course a lot of improvements can be done. But the initial goal to discover the expectimanimin algorithm and the golang bitwise operators are a success. Feel free to leave a message for any questions or suggestions, I’ll be more than happy to answer.
BenchMark
The benchmark has been made in order to compare performance in function of the depth chosen for the algorithm. So the script bench.py has been used to bench the bot. It does 20 runs for each depth from 1 to 8 and make average of each statistic.
Definition of each column:
- depth: the input depth for the bot 2048.
- moves: the average number of moves done for the entire game.
- moves by second: the average speed number of moves by second.
- board eval by move: the average number of board evaluated by the heuristic for each real move.
- time by game: the average time passed for an entire game.
- score: the average score for an entire game.
- 4096,2048,1024: the final values percentage reached.
- win: the percentage of winning games.
| depth | moves | moves by second | board eval by move | time (second) | score | 4096 | 2048 | 1024 | win |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 125.55 | 221515 | 3.47 | 0.00056 | 437.2 | 0% | 0% | 0% | 0% |
| 2 | 116.7 | 38968 | 42.27 | 0.0029 | 430 | 0% | 0% | 0% | 0% |
| 3 | 761.65 | 11482 | 138.36 | 0.066 | 2586.5 | 10% | 30% | 50% | 40% |
| 4 | 813.05 | 1020 | 1789 | 0.6 | 3121 | 13% | 33% | 50% | 46% |
| 5 | 1062 | 256 | 6260 | 4.15 | 3608 | 20% | 60% | 15% | 80% |
| 6 | 1223 | 23 | 75748 | 53.68 | 4208 | 25% | 55% | 20% | 80% |
| 7 | 1528 | 5.89 | 274101 | 259 | 5214 | 55% | 30% | 15% | 85% |
Tracks of improvement
I have identified three main tasks to improve bot 2048 on three different aspects of the code:
- Heuristic: update the evaluation with a free tiles counter to have a penalty for having too few free tiles, since options can quickly run out when the game board gets too cramped.
- Multi threading: For instance, we can parallelized the player’s turn by running 1 thread by move. So the number of moves by second will be increase drastically.
- Expectiminimax: we can reduce the number of nodes and the number of evaluation drastically by stopping the exploration on few criteria, like an evaluation of the board on each node of the tree at each level and keeping only the 10 best evaluations for the player’s turn and the 10 worst for the board’s turn before continuing to the next level.
Feel free to leave a message for any questions or suggestions, I’ll be more than happy to answer, you can also contact me at: contact@algomaths.tech
Thomas Joly
References
- The Mathematics of 2048: Counting States with Combinatorics
- Bitwise operators Golang
- What is the optimal algorithm for the game 2048 ?
- Expectiminimax wikipedia
- 2048 game wikipedia
- Makefile pour Golang